100問マラソン 2問目 SRM 665 Div2 Hard: LuckySum
問題
LuckyNumberは全桁4,7で構成された数字のことを言う.LuckySumとはLuckyNumber2つの和である.
'?'または0-9で構成された文字列(note)が渡されるので,それに一致するような最小のLuckySumを求める.
制約
noteの文字数 <= 14
解法
下の桁から埋めるように全探索.写経.
#include <algorithm> #include <iostream> #include <map> #include <numeric> #include <set> #include <sstream> #include <string> #include <vector> using namespace std; class LuckySum { public: string note; long long INF; long long solve(int n,int up,bool secondEnd) { if(n == -1){ if(up == 0)return 0; return INF; } long long ret = INF; vector<int> sum; if(secondEnd){sum.push_back(4);sum.push_back(7);} else{sum.push_back(11);sum.push_back(14);sum.push_back(8);} for(int i=0;i<sum.size();i++){ sum[i] += up; if( note[n] == '?' || (sum[i]%10+'0') == note[n]){ ret = min(ret, solve(n-1,sum[i]/10,secondEnd) * 10 + (sum[i]-up)); if(!secondEnd) ret = min(ret, solve(n-1,sum[i]/10,true) * 10 + (sum[i]-up)); } } if(n == 0 and up > 0 and (note[0] == '1' or note[0] == '?')) ret = min(ret,solve(n-1,0,secondEnd) * 10 ); return ret; } long long construct(string note) { this->note = note; INF = 1e17; long long res = solve(note.size()-1, 0,false); if(res == INF)return -1; return res; } };
本番中は分岐を全部書こうとして無限に時間を使っていた.こういう書き方できるようになりたい.
これで間に合うのか微妙な気がしたけど間に合うらしい.
100問マラソン 1問目 SRM 666 Div2 Hard: CollectingTokens
問題
木の頂点に得点が設定されており,木の上をL回移動できる時の最高得点を求める.
一度取った頂点の得点を,もう一度取ることはできない.
制約
頂点数 <= 50
L <= 100
解法
解けなかったので,Editorialの解法で書いた.
http://apps.topcoder.com/wiki/display/tc/SRM+666
宝探しページを作った
宝探しページを作りました。
宝探し!
ページのどこかに隠されている合言葉を探し出すというものです。CTFっぽいの。
(まだ、5つしか合言葉はないです。)
ほとんどPHP+MySQLで、
ユーザー管理部分は↓が大変参考になりました。
ユーザー管理をするWebサービスを作ろう (全19回) - プログラミングならドットインストール
Bootstrapでそれっぽいものを作りたいという気持ちの元やってたんですが
PHPとかセッション周りの方がメインになってしまった。
合言葉の隠し方はCTF for ビギナーズの時やったのを幾つか入れています。
たぶん、合言葉はこれから増えていくはずです。
"thank_you_for_reading"
ICPC国内予選 2015
参加まで
サークルのような活動をしていたのでそこにいた先輩2人とチームを組んで、コーチ・監督は研究室の先輩と先生にそれぞれお願いしました。
週1で練習会を開き、本番まで時間があまりなかったので、過去問を2014年〜順々にやっていってました。
感想
僕はA,Bの問題に目を通した後、Cを紙コーディングしてました。
先輩がAをコーディングしているところを横目で見ていたんですが、バグりそうな実装だなぁと思いながらも黙々やってたら、結局バグってしまっていて一旦Aのソースを印刷して、Bをやっていた先輩とバトンタッチ。
Bは比較的すんなりACしてくれて、Aのバグの原因がまだ分かってないようだったので、先にPC借りて紙に書いておいたCを写してAC。
その後、Aも方針を変えて無事AC。
残りの時間はどれも難しいう~んってやってたら時間が終わりました。
Ω\ζ°)チーン
反省
行き当たりばったりで参加を決めた割には(先輩方のおかげで)チームとしてまとまったのではないかと思います。一応目標としていた3完ができたので初参加にしてはなかなか良かったです。
やっぱ先輩主導になっちゃったなぁって感じなので自分のその辺の能力の無さを感じました。
あと、ずっと熱っぽかったし体調管理をしっかりしようと思いました(やっと治りそう)。
Square Route
感想
ACM/ICPC国内予選突破の手引き
で幾何と分類されているけど、幾何ではない気がする。
#include <bits/stdc++.h> using namespace std; typedef long long ll; typedef pair<int,int> P; bool solve(){ int n,m; cin >> n >> m; if(n == 0 && m == 0)return false; vector<int> h(n+1),w(m+1); for(int i=1;i<=n;i++){ cin >> h[i]; h[i] += h[i-1]; } for(int i=1;i<=m;i++){ cin >> w[i]; w[i] += w[i-1]; } vector<int> hei(1500001); for(int i=0;i<=n;i++){ for(int j=i+1;j<=n;j++){ hei[h[j]-h[i]]++; } } int cnt = 0; for(int i=0;i<=m;i++){ for(int j=i+1;j<=m;j++){ cnt += hei[w[j]-w[i]]; } } cout << cnt << endl; return true; } int main(void){ while(solve()){} return 0; }
Problem F Gather the Maps!
感想
誰が誰の地図を持っているかsetで持たせました。
とても遅いし、怪しいところあるけど通ればいいよね。
#include <bits/stdc++.h> using namespace std; typedef long long ll; typedef pair<int,int> P; int main(void){ int n; while(cin >> n, n !=0){ vector<vector<int>> ok(n,vector<int>(31)); bool f = true; for(int i=0;i<n;i++){ int m;cin >> m; for(int j=0;j<m;j++){ int a;cin >> a; ok[i][a] = 1; } } vector<set<int>> st(n); for(int i=0;i<n;i++) st[i].insert(i); for(int i=0;i<31;i++){ vector<int> vec; for(int j=0;j<n;j++){ if(ok[j][i] == 1)vec.push_back(j); } for(int k=0;k<vec.size();k++){ for(int j=k+1;j<vec.size();j++){ st[vec[k]].insert(st[vec[j]].begin(),st[vec[j]].end()); st[vec[j]].insert(st[vec[k]].begin(),st[vec[k]].end()); } } for(int j=0;j<n;j++){ if(st[j].size() == n){ cout << i << endl; f = false; goto END; } } } END: if(f)cout << -1 << endl; } return 0; }
ICPC登録フェイズがきちんと完了できるかがとてつもなく不安です。
NetworkXでグラフを描いた(最短経路他)
研究室の方でNetworkXを教えて頂いたので、試しに色々弄ってみました。
最短経路(ダイクストラ)・経路復元と最長経路(トポロジカルソート+DP)で書いてます。
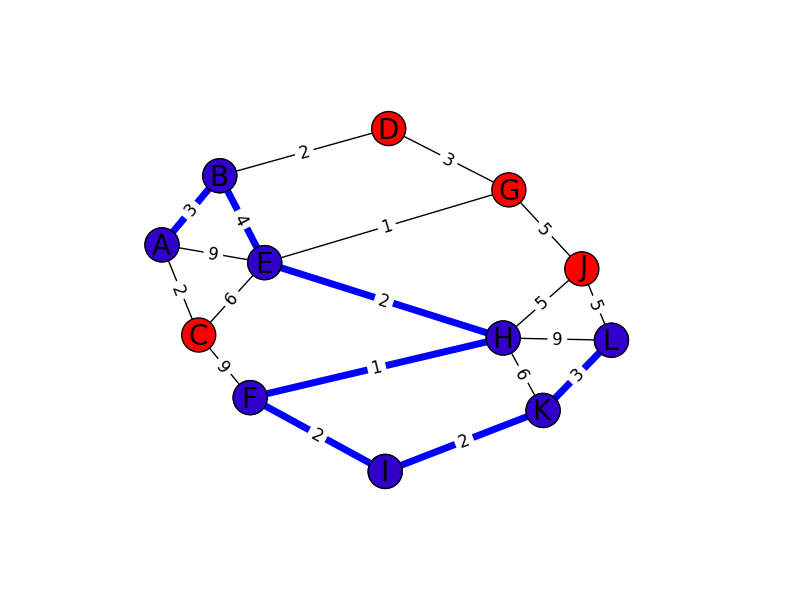
最短経路・経路復元
# -*- coding: utf-8 -*- # Verify(Time Limit Exceeded) # http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=GRL_1_A&lang=jp import networkx as nx import matplotlib.pyplot as plt INF = 1000000 g = nx.Graph() # グラフオブジェクトの生成 # 標準入力から以下の形式で読み込む # |V| |E| # ai bi wi (辺ai->biのweightがwi) V,E = map(int,raw_input().split()) edges = [[] for i in range(V)] # 隣接リスト edge_labels = {} # 辺の描画用のラベル for i in xrange(E): (a,b,w) = map(int,raw_input().split()) g.add_edge(a,b,weight=w) edges[a].append({'to':b,'weight':w}) edges[b].append({'to':a,'weight':w}) edge_labels[(a,b)] = w # Dijkstra from A(0) distance = [INF] * V # Aからの距離 visited = [False] * V # 頂点が訪問済みかどうか distance[0] = 0 for i in range(V): min_v = -1 for v in range(V): # A(0)からの最短頂点を見つける (ヒープを使えば計算量を落とせる) if not visited[v] and (min_v == -1 or distance[v] < distance[min_v]): min_v = v # 訪問済みに visited[min_v] = True # 隣接してる頂点を更新 for e in edges[min_v]: distance[e['to']] = min(distance[min_v] + e['weight'],distance[e['to']]) # 表示 print 'distance from A(0)' for i in range(V): print '%2d: %d' % (i,distance[i]) # trace back from L(11) to A(0) now = 11 path = [11] while now != 0: for e in edges[now]: # labelを利用して経路復元 (頂点更新時に前の頂点を保存しておけば) if distance[now]-e['weight'] == distance[e['to']]: now = e['to'] path.append(now) break print 'trace back from L(11)' print path labels = {} # ノードの描画用のラベル s = list("ABCDEFGHIJKLMNOPQRSTUVWXYZ") for i in range(V): labels[i] = s[i] # distance[i]に変更すれば,ラベルがAからの最短経路長になる # 適当に表示 pos = nx.spring_layout(g) nx.draw_networkx_nodes(g,pos,nodelist=g.nodes(),node_size=600) nx.draw_networkx_edges(g,pos,edgelist=g.edges()) nx.draw_networkx_labels(g,pos,labels,font_size=20) nx.draw_networkx_edge_labels(g, pos, edge_labels=edge_labels,font_size=12) nx.draw_networkx_edges(g,pos,edgelist=[(path[i],path[i+1]) for i in range(len(path)-1)],width=5,edge_color='b') nx.draw_networkx_nodes(g,pos,nodelist=path,node_size=600,node_color='b',alpha=0.8) plt.axis('off') plt.show()
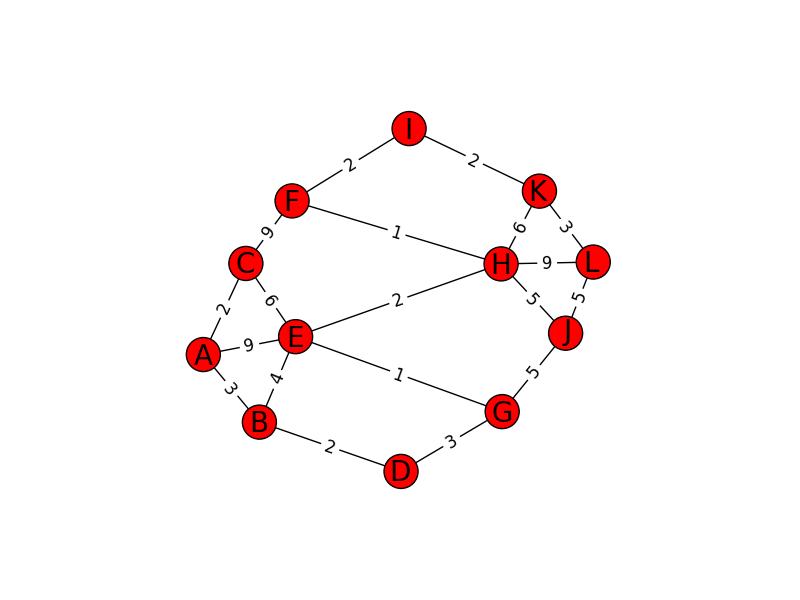
最長経路
# -*- coding: utf-8 -*- import networkx as nx import matplotlib.pyplot as plt import Queue INF = 10000000 class Critical: def __init__(self,v,V,edges): self.v = v self.edges = edges self.tplist = [] # トポロジカルソート def topological_sort(self): visited = [False] * V tplist = [] for i in range(V): if not visited[i]: self.trace(i,visited) self.tplist.reverse() print self.tplist def trace(self,v,visited): visited[v] = True for e in edges[v]: if visited[ e['to'] ]: continue self.trace(e['to'],visited) self.tplist.append(v) # トポロジカル順序で動的計画法 def run(self,s): dp = [0] * V self.topological_sort() for v in self.tplist: for e in edges[v]: dp[e['to']] = max(dp[v]+e['weight'], dp[e['to']]) print dp return dp # Dijkstraっぽく最長ノードを使っていくのは駄目 def run2(self,s): dp = [INF] * V visited = [False] * V q = Queue.PriorityQueue() q.put((0,s)) dp[s] = 0 while not q.empty(): d,v = q.get() visited[v] = True for e in edges[v]: if visited[e['to']] or dp[v]+e['weight'] > dp[e['to']]: continue dp[e['to']] = dp[v] + e['weight'] q.put((d-e['weight'],e['to'])) print dp return dp V,E = map(int,raw_input().split()) edges = [[] for i in range(V)] #隣接リスト edge_labels = {} # 辺の描画用のラベル g = nx.DiGraph() #有向グラフの生成 for i in xrange(E): (a,b,w) = map(int,raw_input().split()) g.add_edge(a,b,weight=w) edges[a].append({'to':b,'weight':w}) edge_labels[(a,b)] = w # critical path cr = Critical(0,V,edges) cr.run2(0) distance = cr.run(0) labels = {} # ノードの描画用のラベル s = list("ABCDEFGHIJKLMNOPQRSTUVWXYZ") for i in range(V): labels[i] = s[i] #s[i] を distance[i]に変えれば,最長距離がノードのラベル # 適当に表示 pos = nx.spring_layout(g) nx.draw_networkx_nodes(g,pos,nodelist=g.nodes(),node_size=600) nx.draw_networkx_edges(g,pos,edgelist=g.edges()) nx.draw_networkx_edge_labels(g, pos, edge_labels=edge_labels,font_size=12) nx.draw_networkx_labels(g,pos,labels,font_size=20) plt.axis('off') plt.show()
上2つのコードでは、特に下のグラフ中でのAからLについて考えていて、A~Lに0~11を対応させています。
標準入力用ファイル
12 19 0 1 3 0 2 2 0 4 9 1 3 2 1 4 4 2 4 6 2 5 9 3 6 3 4 6 1 4 7 2 5 7 1 5 8 2 6 9 5 7 9 5 7 11 9 7 10 6 8 10 2 9 11 5 10 11 3
グラフを描画する時、適当な位置に頂点を配置してくれるのは嬉しいけど、やや面倒くさい(もっと良いやり方があるのかも)
頂点の配置のアルゴリズムもそのうち確認しておきたい。
Pythonでグラフ系のものを書くのは初めてだったので、勉強になりました。言語的に間違っているのか、書いたアルゴリズムが間違ってるのか特定できず、割りと時間がかかってしまった。