NetworkXでグラフを描いた（最短経路他）

研究室の方でNetworkXを教えて頂いたので、試しに色々弄ってみました。
最短経路(ダイクストラ)・経路復元と最長経路(トポロジカルソート+DP)で書いてます。

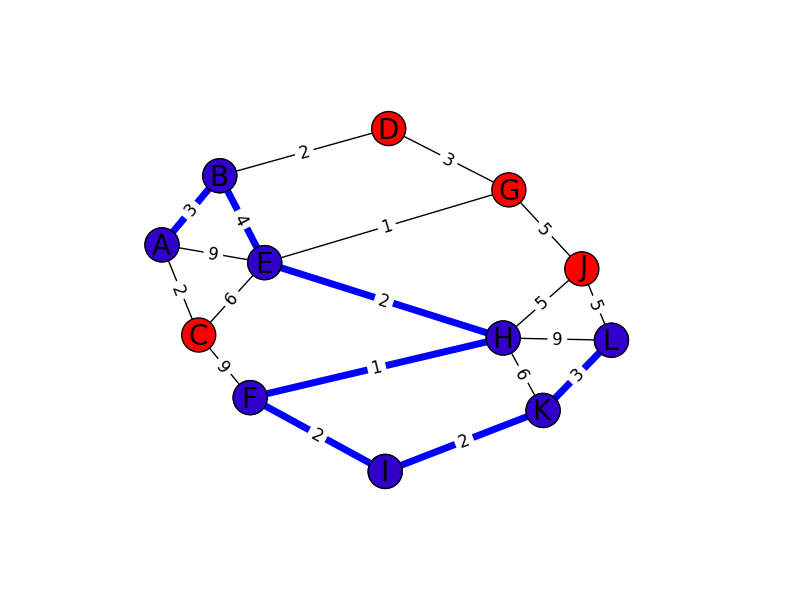
最短経路・経路復元

# -*- coding: utf-8 -*-
# Verify(Time Limit Exceeded)
# http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=GRL_1_A&lang=jp
import networkx as nx
import matplotlib.pyplot as plt

INF = 1000000
g = nx.Graph()	# グラフオブジェクトの生成
# 標準入力から以下の形式で読み込む
# |V| |E|
# ai bi wi (辺ai->biのweightがwi)
V,E = map(int,raw_input().split())
edges = [[] for i in range(V)]	# 隣接リスト
edge_labels = {}	# 辺の描画用のラベル
for i in xrange(E):
	(a,b,w) = map(int,raw_input().split())
	g.add_edge(a,b,weight=w)
	edges[a].append({'to':b,'weight':w})
	edges[b].append({'to':a,'weight':w})
	edge_labels[(a,b)] = w

# Dijkstra from A(0)
distance = [INF] * V	# Aからの距離
visited = [False] * V	# 頂点が訪問済みかどうか
distance[0] = 0
for i in range(V):
	min_v = -1
	for v in range(V):
		# A(0)からの最短頂点を見つける (ヒープを使えば計算量を落とせる)
		if not visited[v] and (min_v == -1 or distance[v] < distance[min_v]):
			min_v = v
	# 訪問済みに
	visited[min_v] = True
	# 隣接してる頂点を更新
	for e in edges[min_v]:
		distance[e['to']] = min(distance[min_v] + e['weight'],distance[e['to']])
# 表示
print 'distance from A(0)'
for i in range(V):
	print '%2d: %d' % (i,distance[i])

# trace back from L(11) to A(0)
now = 11
path = [11]
while now != 0:
	for e in edges[now]:
		# labelを利用して経路復元 (頂点更新時に前の頂点を保存しておけば)
		if distance[now]-e['weight'] == distance[e['to']]:
			now = e['to']
			path.append(now)
			break
print 'trace back from L(11)'
print path

labels = {}	# ノードの描画用のラベル
s = list("ABCDEFGHIJKLMNOPQRSTUVWXYZ")
for i in range(V):
	labels[i] = s[i] # distance[i]に変更すれば,ラベルがAからの最短経路長になる

# 適当に表示
pos = nx.spring_layout(g)
nx.draw_networkx_nodes(g,pos,nodelist=g.nodes(),node_size=600)
nx.draw_networkx_edges(g,pos,edgelist=g.edges())
nx.draw_networkx_labels(g,pos,labels,font_size=20)
nx.draw_networkx_edge_labels(g, pos, edge_labels=edge_labels,font_size=12)

nx.draw_networkx_edges(g,pos,edgelist=[(path[i],path[i+1]) for i in range(len(path)-1)],width=5,edge_color='b')
nx.draw_networkx_nodes(g,pos,nodelist=path,node_size=600,node_color='b',alpha=0.8)

plt.axis('off')
plt.show()

最長経路

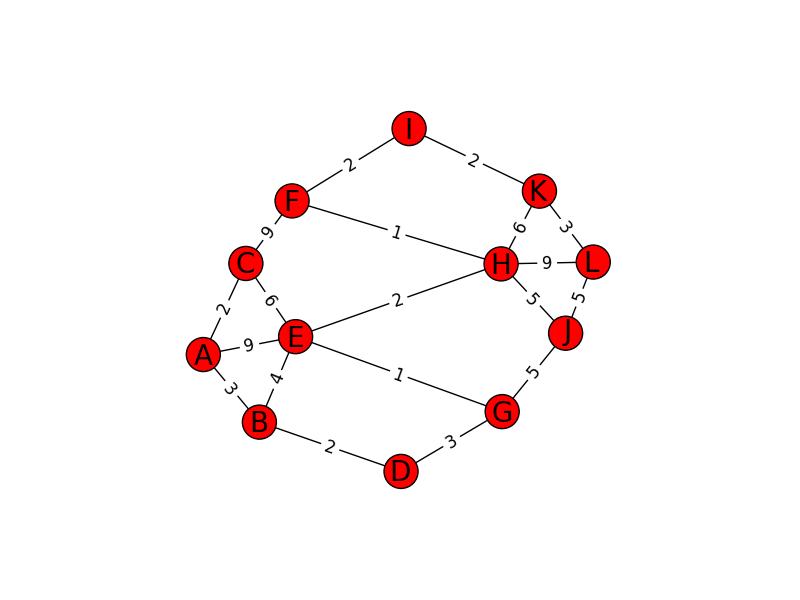
# -*- coding: utf-8 -*-
import networkx as nx
import matplotlib.pyplot as plt
import Queue
INF = 10000000

class Critical:
	def __init__(self,v,V,edges):
		self.v = v
		self.edges = edges
		self.tplist = []

	# トポロジカルソート
	def topological_sort(self):
		visited = [False] * V
		tplist = []
		for i in range(V):
			if not visited[i]: self.trace(i,visited)
		self.tplist.reverse()
		print self.tplist

	def trace(self,v,visited):
		visited[v] = True
		for e in edges[v]:
			if visited[ e['to'] ]:
				continue
			self.trace(e['to'],visited)
		self.tplist.append(v)

	# トポロジカル順序で動的計画法
	def run(self,s):
		dp = [0] * V
		self.topological_sort()
		for v in self.tplist:
			for e in edges[v]:
				dp[e['to']] = max(dp[v]+e['weight'], dp[e['to']])
		print dp
		return dp

	# Dijkstraっぽく最長ノードを使っていくのは駄目
	def run2(self,s):
		dp = [INF] * V
		visited = [False] * V
		q = Queue.PriorityQueue()
		q.put((0,s))
		dp[s] = 0
		while not q.empty():
			d,v = q.get()
			visited[v] = True
			for e in edges[v]:
				if visited[e['to']] or dp[v]+e['weight'] > dp[e['to']]: continue
				dp[e['to']] = dp[v] + e['weight']
				q.put((d-e['weight'],e['to']))
		print dp
		return dp

V,E = map(int,raw_input().split())
edges = [[] for i in range(V)]		#隣接リスト
edge_labels = {}	# 辺の描画用のラベル

g = nx.DiGraph()	#有向グラフの生成
for i in xrange(E):
	(a,b,w) = map(int,raw_input().split())
	g.add_edge(a,b,weight=w)
	edges[a].append({'to':b,'weight':w})
	edge_labels[(a,b)] = w

# critical path
cr = Critical(0,V,edges)
cr.run2(0)
distance = cr.run(0)

labels = {}	# ノードの描画用のラベル
s = list("ABCDEFGHIJKLMNOPQRSTUVWXYZ")
for i in range(V):
	labels[i] =  s[i] #s[i] を distance[i]に変えれば,最長距離がノードのラベル

# 適当に表示
pos = nx.spring_layout(g)
nx.draw_networkx_nodes(g,pos,nodelist=g.nodes(),node_size=600)
nx.draw_networkx_edges(g,pos,edgelist=g.edges())
nx.draw_networkx_edge_labels(g, pos, edge_labels=edge_labels,font_size=12)
nx.draw_networkx_labels(g,pos,labels,font_size=20)
plt.axis('off')
plt.show()

上2つのコードでは、特に下のグラフ中でのAからLについて考えていて、A~Lに0~11を対応させています。

標準入力用ファイル

12 19
0 1 3
0 2 2
0 4 9
1 3 2
1 4 4
2 4 6
2 5 9
3 6 3
4 6 1
4 7 2
5 7 1
5 8 2
6 9 5
7 9 5
7 11 9
7 10 6
8 10 2
9 11 5
10 11 3

グラフを描画する時、適当な位置に頂点を配置してくれるのは嬉しいけど、やや面倒くさい（もっと良いやり方があるのかも）
頂点の配置のアルゴリズムもそのうち確認しておきたい。

Pythonでグラフ系のものを書くのは初めてだったので、勉強になりました。言語的に間違っているのか、書いたアルゴリズムが間違ってるのか特定できず、割りと時間がかかってしまった。